时间轮算法

时间轮算法是为了应对定时器的数量越来越多的情况，在待处理定时器的总数达到几千个甚至上万个时，我们希望定时器的性能仍有保证，定时器的性能要从时间复杂度和空间复杂度两方面考虑。

时间复杂度分析主要包括以下几种操作：

• 定时器启动：定时器在启动时需要提供超时时间和超时回调函数，并且一般会返回一个用于标识定时器的id。
  
• 定时器取消：定时器在取消时将指定id的定时器移除。
  
• 定时器超时判断：超时判断会有一个检查周期（频率），在每次检查中会找出需要超时触发的定时器。
  

空间复杂度指定时器在存储时所消耗的内存，主要受存储时使用的数据结构影响。

一般来讲，时间复杂度和空间复杂度是紧密联系在一起的，并且鱼和熊掌不可兼得，通常需要牺牲一方面性能换取另一方面性能的提升。很显然，定时器是一个对时间很敏感的功能，在定时器调度策略中，我们在考虑时倾向于牺牲空间性能换取时间性能。

在实现前需要假定所有定时器的超时时间（周期数量）都不会超过某个最大值 N ，这样我们可以用一个容量为 N 的环形链表存放定i时器，每个链表节点对应一个超时时间，将所有超时时间相同的定时器存放在同一个链表节点中。链表中有一个节点代表当前时间 i ，在每次执行检查时将当前时间 i 向前移动移动一个节点变成 i+1 节点， 这样 i+1 节点中的所有定时器就需要超时触发了。在添加一个超时时间为 t 新的定时器时，需要将其放在第 (i+t)%N 个节点中。

举一个简单的例子，如下图所示，假设 N 为8且 i 为1，形象地讲就是最大超时时间为8秒，每一个小格代表1秒。在左面的图中，当前时间对应的第1格是第1秒，该节点中所有的定时器执行超时回调函数。在右面的图中，经过1秒后到达了下一个检查周期，即第2秒对应的第2格中的所有定时器超时触发，它们的回调函数会被执行。

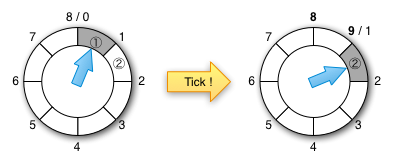
配图来源：confluent.io

当最大超时时间 N 很大时，基础时间轮中的节点增多，这样会消耗很多内存。我们可以将相邻的定时器归为一组，将这一组作为一个时间轮节点。每次在定时器超时判断时只需关注当前节点中的那一组定时器。这种方法借鉴了哈希运算的思想，可以看作是一种广义上的哈希运算，就是将变化范围大的对象经过哈希函数映射到一个较小的范围。

当然每个节点中定时器的组织方法可以有很多种，如：不排序的链表、排序的链表、优先队列，这部分的处理策略其实就是一个缩小版定时器调度处理。

分层时间轮算法可以看作是哈希时间轮算法的一个特例，即哈希时间轮中的每个节点中存放的仍然是时间轮。以我们生活中的常见的钟表为例：有24个节点表示小时，每个节点表示1小时；小时节点中有60个分钟节点，每个分钟节点表示1分钟；分钟节点中有60个秒节点，每个秒节点表示1秒。其中的时、分、秒就是将时间轮分为了3个层次。

上面提到的时间轮算法的几个变体是空间与时间转换的典型案例。为了使每次超时判断处理的速度变快，将定时器按照超时时间分开，这样每次只需要关注那一小部分快要超时的定时器，这是空间换时间。为了减少存储定时器所需要内存，将超时时间接近的放在一个节点中，这是时间换空间。而分层时间轮其实就是每层的节点中仍然是时间轮，这又使用是递归思想。仔细品味算法的设计思路，还真的是蛮有意思的。

我找了几个时间轮算法的实现代码，不过没有深入研究，等以后有时间的时候再仔细看看：

• github - skywind3000 AsyncNet
  
• github - wahern timeout
  

• columbia edu - timing wheel
  
• acolyer blog - hashed and hierarchical timing wheel
  

（全文完）